在这个以及后面的一些博客里，我们将会讲解运动学逆解算问题(IK问题)-当然，大部分是使用雅可比矩阵来求解的。尽管这个方法应该有许多计算，但是我们可以仅仅把必要的理论展示出来；不需要多少计算，只要一些微积分、矩阵运算、矢量叉乘等运算方式的知识，我们就可以进入讲解了。（当然，还需要理解一些欧式变换的矩阵形式，比如平移，旋转，仿射变换等）
首先，我们在这一页会讲解基础的运动学正解算和逆解算的式子，然后下一页我们会讨论一些雅可比矩阵的意义（比如雅可比矩阵的逆）来解决这些问题。
广义上来说，可以参考论文Inverse Kinematics: a review of existing techniques and introduction of a new fast iterative solver。
也就是说，IK问题能够让物体从一个位置移动到另一个位置。比如你想拿起桌子上的一杯水，你的大脑就会解算一系列抽象的运动学逆解问题：比如如何移动你的肩关节，肘关节，和手腕来让你的手到达水杯所在的位置。
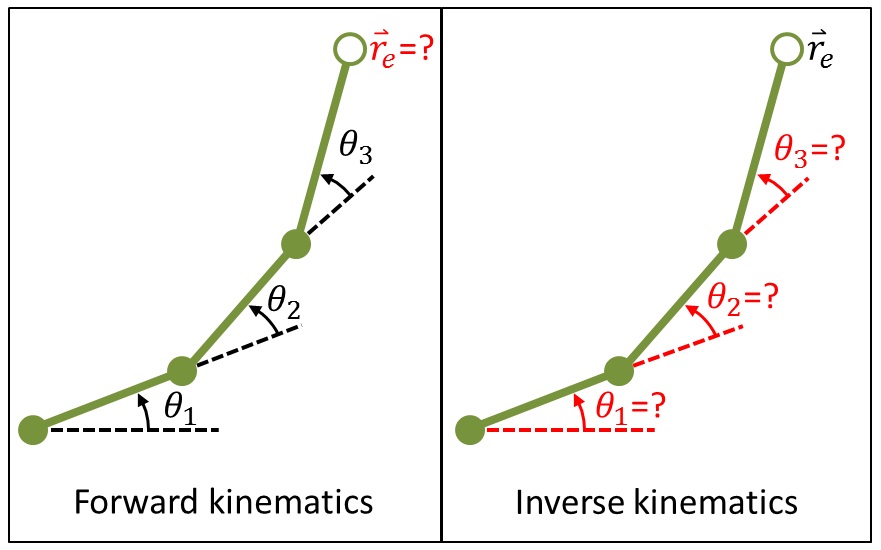
在机器人运动学中，机械臂的控制就需要这一系列运动学逆解算。这里的IK问题，指的是Inverse Kinematics问题，正好是Forward Kinematics问题的逆命题。
假如我们有一个2D平面内的多连杆机械臂并由许多可旋转的关节组成，终端为机械夹爪或者其他操作工具（比如铣刀等）。
同时假设每一个机械臂关节的关节角 \(\theta_i\) 和杆长 \(L\) 最终就能计算得出终端位置 \(\mathbf{r}_e\) 。 这就是运动学正向问题(Forward Kinematics).
那么同理，你应该可以很容易得出运动学逆解算(Inverse Kinematics):已知终端位置 \(\mathbf{r}_e\) 应该如何计算出每一个关节角 \(\theta_i\) 来达到终端位置。
易知，运动学正解问题(FK问题)只有一个解(unique solution)，但是运动学逆解算(IK问题)一般就不只有一个解(Many solutions)。
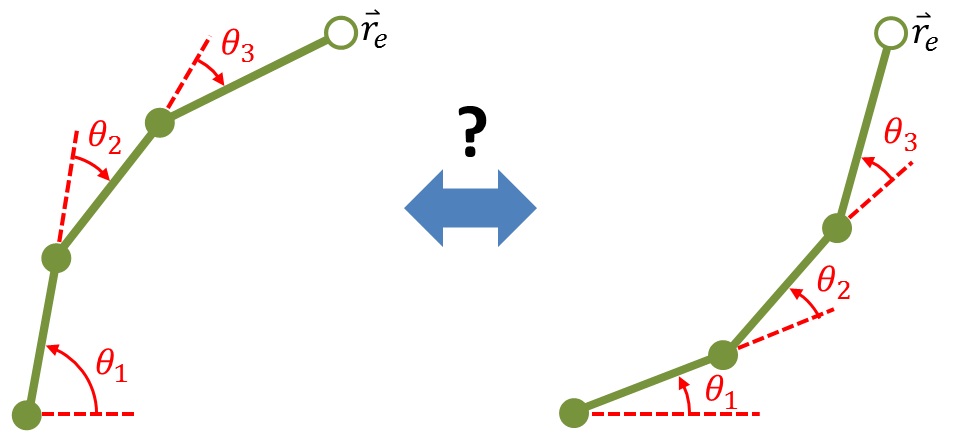
由于对称性，我们就可以到达相同的位置有许多不同的解法，这样我们就会得到多解问题。下面我们就将数学描述一下机械臂，建立相关的数学模型:
我们机械臂中有许多旋转的部分，那么我们自然想到为每个关节定义一个坐标系:
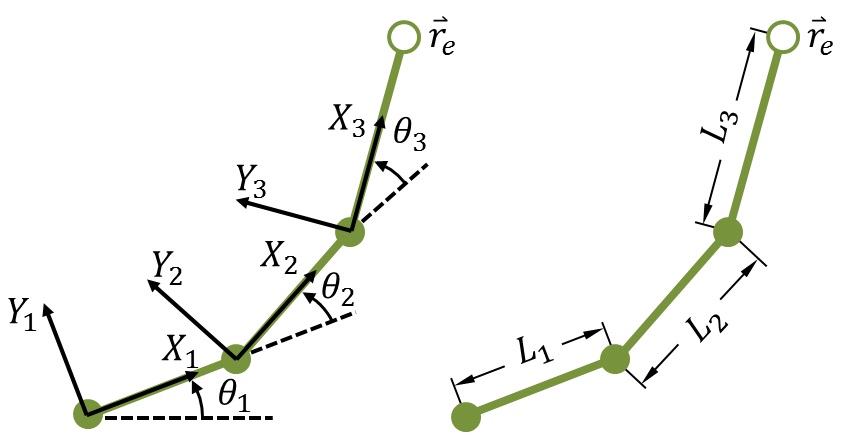
这种情况下，我们每一个关节都是自己坐标系下的远点，那么\(X1Y1\)这个坐标系就是第一个关节的坐标系， \(X_1\)沿着\(L_1\)方向，同时第一个坐标系旋转了 \(\theta_1\) 角度，此后每个坐标系相同，不难有\(X_iY_i\)长度\(L_i\)，旋转了\(\theta_i\)。
接下来我们定义世界坐标系(Global coordinate system)\(X_0Y_0\)，随后由欧式坐标变换矩阵可以得出:
\[{}_0^3P={}_0^1T{}_1^2T{}_2^3T P_0\]
其中由矩阵变换不难有:
\[[{}^1_0
T]=\begin{bmatrix}\cos\theta_1&-\sin\theta_1&0&x_0\\
\sin\theta_1& \cos\theta_1&0&y_0\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}\] \[
[{}^2_1 T]=\begin{bmatrix}
\cos\theta_2 &-\sin\theta_2 & 0& L_1\\
\sin\theta_2& \cos\theta_2&0 &0\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}
\] \[
[{}^3_2 T]=\begin{bmatrix}\cos\theta_3&-\sin\theta_3&0&L_2\\
\sin\theta_3& \cos\theta_3&0&0\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}
\] \[
[P_0]=\begin{bmatrix}L_3 &0 &0 &1\end{bmatrix}^T
\] 最终有结果:\(\mathbf{r}_e=[{}^1_0
T][{}^2_1 T][{}^3_2 T][P_0]\) # 雅可比矩阵前置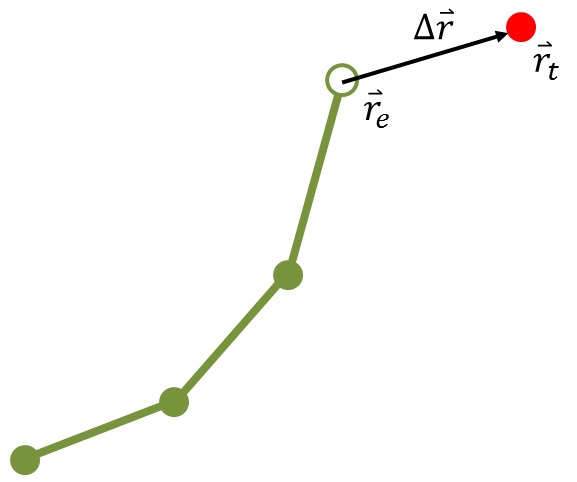 
我们目标是为了确定终端位置如何从一个位置\(\mathbf{r}_e\)移动到另一个位置\(\mathbf{r}_t\)，那么我们就有了一个微小的\(\Delta\mathbf{r}=\mathbf{r}_e-\mathbf{r}_t\)，这样我们就可以引入雅可比矩阵来进行后面的的求解(其实也就是用每个关节角的改变\(\Delta \theta来进行终端位置的仿真)\)了。 #
雅可比矩阵
雅可比矩阵可以用来处理多变量函数的斜率，使用矩阵形式；当然，雅可比矩阵很自然的会有如下构造:
\[\mathbf{\Delta}\mathbf{r}=\mathbf{J}\mathbf{\Delta}\mathbf{\theta}\]
但是\(\mathbf{J}\)到底代表什么呢?在三维平面内，雅可比矩阵是一个\(3\times n\) 的矩阵，n代表机械臂的个数: 
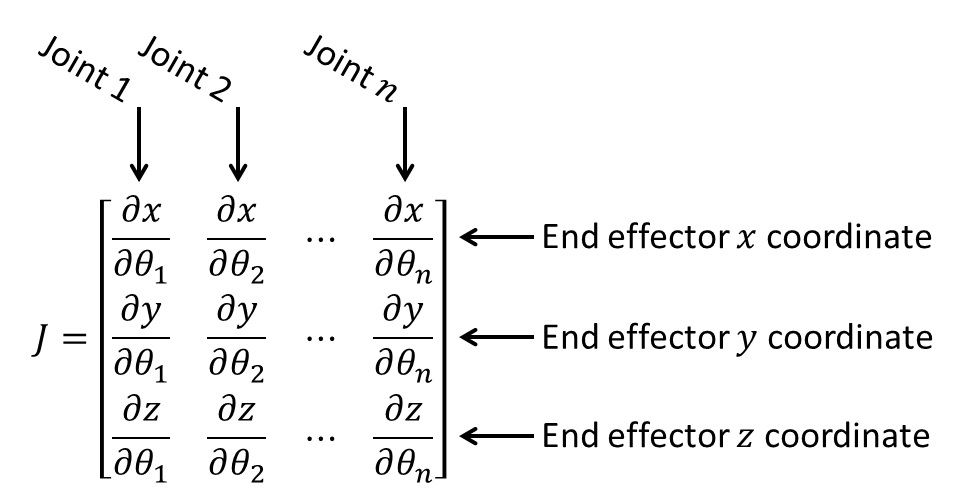这个矩阵表示了机械臂末端位置坐标(x,y,z)关于每一个机械臂的关节角的变化。
那么我们有:
\[\Delta \overrightarrow{r}=\left\{ \begin{matrix}\Delta x \\ \Delta y \\ \Delta z\end{matrix}\right\}=\begin{bmatrix}\frac{\partial x}{\partial \theta_1} &\frac{\partial x}{\partial \theta_2} &\cdots &\frac{\partial x}{\partial \theta_n}\ \\\frac{\partial y}{\partial \theta_1} &\frac{\partial y}{\partial \theta_2} &\cdots &\frac{\partial y}{\partial \theta_n}\ \\\frac{\partial z}{\partial \theta_1} &\frac{\partial z}{\partial \theta_2} &\cdots &\frac{\partial z}{\partial \theta_n} \end{bmatrix}\left\{ \begin{matrix}\Delta \theta_1 \\ \Delta \theta_2\\\vdots \\ \Delta \theta_n\end{matrix}\right\}=\left\{ \begin{matrix}\frac{\partial x}{\partial \theta_1}\Delta\theta_1 &\frac{\partial x}{\partial \theta_2}\Delta\theta_2 &\cdots &\frac{\partial x}{\partial \theta_n}\Delta\theta_n \\\frac{\partial y}{\partial \theta_1}\Delta\theta_1 &\frac{\partial y}{\partial \theta_2}\Delta\theta_2 &\cdots &\frac{\partial y}{\partial \theta_n}\Delta\theta_n \\\frac{\partial z}{\partial \theta_1}\Delta\theta_1 &\frac{\partial z}{\partial \theta_2}\Delta\theta_2 &\cdots &\frac{\partial z}{\partial \theta_n}\Delta\theta_n\end{matrix}\right\} \]
另一种解释为:
这个雅可比矩阵运算的结果表示每一个机械臂的终端位置，比如下图中第一个，这个也就是\(\theta_1\)的影响；下图所有的虚线分别表示改变\(\theta_i\)导致末端位置的改变，箭头表示后面机械臂整体运算出的结果(可以视为这一个机械臂连杆旋转所经过的轨迹)。
不难发现，只要我们对终端位置(x,y,z)取关于每个关节角度\(\theta_i\)的微分，那么我们最终属于是线性化了这个问题（也就是说，你只需要解一个线性方程组即可）。但是，这种方法因为所取为微分，所以对于较大角度的改变可能不是那么精确。
那么我们应该如何得出雅可比矩阵的每个元素呢？，一种方式是通过欧式坐标变换矩阵来得到一个终端位置(x,y,z)关于每个关节角\(\theta_i\)的函数:\(\mathbf{r}_e=f(\mathbf{\theta})=f(\theta_1,\theta_2,\theta_3,\cdots,\theta_n)\)，这个式子我们已经在前面写出过了。
那么另一种方法就是通过叉乘: \[\frac{\partial \mathbf{r_e}}{\partial \theta_j}=\mathbf{a_j}\times (\mathbf{r_e}-\mathbf{r_j})\] 这里的\(\theta_j,\mathbf{r_j}\)表示第j个关节的夹角与位置，\(\mathbf{a_j}\)表示这个关节轴的旋转矢量。
那么如果这么定义: \[\mathbf{J}=\left[\begin{matrix}{\mathbf{a_1}\times (\mathbf{r_e}-\mathbf{r_1})}^T &{\mathbf{a_2}\times (\mathbf{r_e}-\mathbf{r_2})}^T&{\mathbf{a_3}\times (\mathbf{r_e}-\mathbf{r_3})}^T &\cdots &{\mathbf{a_n}\times (\mathbf{r_e}-\mathbf{r_n})}^T\\ \end{matrix}\right]\] 对于二维XY平面内的机械臂，旋转矢量始终指向Z轴方向，因此，我们旋转矢量\(\mathbf{a_j}=\alpha \hat{k}\)
那么为了构造这种雅可比矩阵，我们需要使用一些求逆方法；当然，大部分雅可比矩阵都不是平方项，所以大部分不可逆；为了避免求逆问题的存在，我们需要使用广义逆-伪逆矩阵(当然我们不讲述这个，只是用来保证一定可以求逆即可)。
我们通过逆矩阵就能写出: \[\mathbf{J}^{-1}\mathbf{\Delta}\mathbf{r}=\mathbf{\Delta}\mathbf{\theta}\] 根据这个式子我们就不难得出每个关节角角度。
雅可比矩阵这里写下的\(3\times n\)的形式其实是简化后的，这个形式一般只是用来得出终端位置。如果我们需要机械臂的终端位置与终端朝向，那么我们要使用\(6\times n\)的形式，其中第4，5，6三行应该表示机械臂终端关于X,Y,Z轴旋转的过程。
当然，我们就可以给出映射关系(相应的眼科比矩阵的第i列表示): \[\mathbf{J_i}=\left\{\begin{matrix}\begin{bmatrix}{}^BZ_i\\0\end{bmatrix}&,i为移动关节\\\begin{bmatrix}{}^BZ_{i}\times ({}^B_iR^{i}p_n)\\{}^BZ_{i}\end{bmatrix}&,i为旋转关节\end{matrix}\right.\] 对于移动关节:\(Z_i\)表示第i个坐标系中Z轴单位向量在基坐标系{0}中的表示。 对于转动关节:\({}^BZ_{i-1}\)表示是坐标系{i}的z轴单位向量在基座标系{0}中的表示。 \(p_{in}^0={}^B_iR^ip_n\)表示末端坐标原点相对坐标系{i}的位置矢量在基座标系{0}中的表示。